- Why Learn Trigonometry?
- The Flash Coordinate System
- Anatomy of a Triangle
- The Pythagorean Theorem
- The Heart of Trig
- Vectors
- Points to Remember
The Flash Coordinate System
The coordinate system used in Flash is called the Cartesian coordinate system. (This may sound vaguely familiar to you from math classes, and if so, the information here should be a simple review.) Understanding how the Cartesian coordinate system is set up and how to use it is very important for a game developer. Why, exactly? Because in your games you will be creating and moving objects around the screen, using ActionScript to tell an object which coordinates to move to. And to write ActionScript that does this, you've got to have an understanding of the coordinate system. In this section I'll (re)acquaint you with this all-important grid. We'll also discuss how the Flash coordinate system measures angles.
Cartesian Coordinates
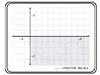
The Cartesian coordinate system is grid-based (made up of many equal-sized imaginary squares), with a horizontal axis called the x-axis and a vertical axis called the y-axis.
The way we look at this grid in Flash positions the negative side of the y-axis higher than the positive side.
Actually, there is no difference at all between the two coordinate systems you've just seen. What is different is how we are observing them. If you stand on your head to view an object, then only the way you are observing it has changed, not the object itself. That is what's happening here. In math class you observed the coordinate system one way; in Flash, you will observe it upside-down and backwards.
Most computer programs use the same orientation of the coordinate system as Flash does. If you have a window open on your computer, you can grab on to a corner to resize it. The contents of the window may resize, or perhaps the amount of content shown changes. But what does not change is the upper-left corner of the window. That corner is designated as the origin—the point where the x-axis and y-axis cross. Then all of the contents are contained within the +x and +y quadrant. If the origin were always, say, in the center of the screen, then as you resized the window the coordinates of every element in your window (images or movie clips) would change. A top-left-origin coordinate system is a great convenience.
A Cartesian coordinate is a set of two numbers that describe the position of a point. In math, the two numbers in the coordinate are usually grouped in parentheses, like this: (4, 8). The 4 represents a distance along the x-axis, and the 8 represents a distance along the y-axis.
Movie-Clip Coordinate Systems
As you've learned in this section, the origin of Flash's coordinate system is the upper-left corner of the Flash movie. Every individual movie clip also has its own coordinate system (called a relative coordinate system). The origin for movie clips is called, in Flash terminology, a registration point. At this point in the book, it is just important to know that movie clips contain their own coordinate systems. In later chapters we will make use of these movie-clip coordinate systems.
Angles
Angles are used in two ways in Flash: They are used to rotate objects, and they are used with the trigonometric functions that will be discussed later in this chapter. But before you can use angles to do anything, you need to understand how they are measured in the Flash coordinate system.
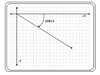
Positive angles are measured from the x-axis, rotated in a clockwise direction, and with a fixed point at the origin.
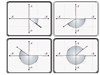
Angles are measured in degrees and can have a value of 0° to 360°. The entire coordinate system is made up of four quadrants separated by the axes. Each quadrant covers 90°.
More on Angles
Angle measurements are repeating—that is, you can never have an angle greater than 360°. So let's say you have an object that may have actually rotated 720°—two full rotations. That is possible, of course, but its orientation is still 360°. (You determine the end orientation of an angle by subtracting 360 from the total number until it becomes less than or equal to 360.)
Negative angles are also possible. But that description doesn't mean the angle itself is negative, or inverted (that wouldn't make any sense). The negative number merely tells you that the angle was measured counterclockwise from the x-axis.
In addition to degrees, there is another common way to measure angles: in radians. One full rotation is 2p radians. With degrees, we know that one rotation is 360°, so each quarter rotation is 90°. Likewise, with radians, since a full rotation is 2p, each quarter rotation is p/2. For those who may not remember, p (pi, or Math.PI in ActionScript) is a special number in math, representing the ratio of the circumference of a circle to its diameter. Rounded to two places, it is 3.14. Pi can be accessed in Flash by using Math.PI. For example, here is a way to create a variable that has the value of pi:
myPI = Math.PI;
So why do you need to know about radians? Because everything you do in Flash with angles—with one exception—needs to be expressed in radians.
Unlike degrees, which are arbitrary, radians form a "natural" unit measurement. The word natural here means a unit that (through the use of mathematical theory) has been found convenient and logical. That's probably why mathematicians, physicists, and programmers like radians better, and use them almost exclusively.
The only time you can use degrees directly in Flash is when you're changing the _rotation property of a movie clip. However, human nature and habit being what they are, it is very common (and perfectly all right) to work with degrees in ActionScript, and then convert from degrees to radians just before you need to use the angle. Converting degrees to radians or radians to degrees is easy.