Create Primitives and Text in Maya 7
Primitives are pre-made geometry sets, usually in simple shapes: spheres, cubes, cylinders, planes, cones, and toruses ( Figure 3.1 ). New in Maya 7.0, you can also create more unusual polygon primitives: prisms, pyramids, pipes, helixes, soccer balls, and platonic solids ( Figure 3.2 ).

Figure 3.1 The basic primitives (clockwise, from top left): sphere, cube, cylinder, torus, plane, cone.

Figure 3.2 Maya 7.0's new polygon primitives (clockwise, from top left): prism, pyramid, pipe, platonic solid, soccer ball, helix.
Primitives are the building blocks of 3D modeling, simplifying the creation of more complex objects. Some real-world objects can be constructed out of a single primitive shape: a baseball is a sphere, an unopened book is a scaled cube, and a box of doughnuts is a box of toruses. Other objects combine a number of different primitives. For example, a bicycle wheel combines thin cylinders for the spokes and hub with toruses for the rim and tire ( Figure 3.3 ).
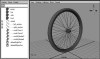
Figure 3.3 This bicycle wheel is made from cylinder and torus primitives.
Not everything is made out of primitives, but Maya's modeling tools allow you to modify primitives so extensively that you can make nearly any shape by starting with primitives. This makes them valuable time savers for almost any modeling task. If your scene needs text, you can also save time by using Maya's text tool, which automatically generates geometry for the text you enter.
Maya's construction history feature allows you to change the attributes of primitives and other objects after you've created them. You can also rename them to make management of your scene simpler.
About Primitive Types
Maya includes three primary types of primitives: NURBS, polygons, and subdivs. Each of these types has its own strengths and weaknesses, making them appropriate for different types of models.
About NURBS
NURBS stands for Non-Uniform Rational B-Spline, which describes the mathematical nature of this type of object. Topologically, a NURBS surface is always a single surface with four edges, like a sheet of paper, which can be curved and stretched into different shapes ( Figure 3.4 ).

Figure 3.4 A NURBS torus, like all NURBS surfaces, is made from a single sheet of geometry.
NURBS can provide smooth surfaces with relatively few control vertices, so you can easily control the general shape of the object. However, your ability to selectively add detail to a NURBS surface is limited, because its control points must always form a grid (even if it's a highly distorted grid). As a result, you can only increase the number of control vertices by increasing them across the surface in one or both directions. Also, because of NURB surfaces' simple topology ( Figure 3.5 ), many objects require more than one NURBS surface. This makes NURBS inconvenient to use, if not impossible, for many types of objects. However, for simple objects, they provide a quick and easy way to create smooth surfaces.
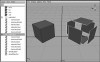
Figure 3.5 Due to the inherent limitations of NURBS surfaces, a NURBS cube primitive is constructed from six surfaces, one for each side.
NURBS primitives are most useful when you intend to use them as primitives, alone or in combination, rather than modify them to create other shapes. For more information on NURBS objects, see Chapter 7.
About polygons
Polygons are flat surfaces defined by three or more vertices, or points ( Figure 3.6 ). By using Maya's tools to create many connected polygons, you can produce high-quality, smooth surfaces. Using fewer polygons results in low-resolution, fast-rendering surfaces ( Figure, 3.7 ).
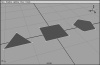
Figure 3.6 Three and four-sided polygons are most common, but polygons can have any number of points.

Figure 3.7 The sphere on the left is smoother, but the lower-resolution sphere on the right will render faster.
Unlike NURBS, you can create a shape with any topology as a single polygonal mesh, and you can add detail to the specific areas that need it. However, because the number of vertices increases with the number of polygons in an object, adjusting a polygonal object's general shape can be more time-consuming than doing so for an equivalent NURBS surface ( Figure 3.8 ).

Figure 3.8 A NURBS sphere (left) can be shaped into an egg by scaling the upper control vertices. A polygonal sphere (right) needs more vertices to be smooth, so it can't be reshaped as easily.
Polygon primitives are most useful as a starting point for creating more complex polygonal models, especially relatively low-resolution models. For more information on polygonal modeling, see Chapter 8.
About subdiv surfaces
Subdivision surfaces, or subdivs, combine the best aspects of both NURBS and polygons. Like a polygonal object, a subdiv surface uses only one mesh to define complex surfaces, and it provides the same smoothness and high-level control as a NURBS surface ( Figure 3.9 ).

Figure 3.9 The mug on the left is a subdiv surface. The mug on the right is the equivalent polygonal mesh.
Although subdivs have been around since 1978, computer hardware has only recently become fast enough to make working with them manageable. Depending on the complexity of your model and the processing power of your computer, subdivision surfaces can be significantly slower to manipulate and render than NURBS or polygons.
Subdiv primitives, like polygons, are most useful as a starting point for creating more complex models. Subdivision surfaces are particularly useful for high-resolution work. For more information on subdiv modeling, see Chapter 9.