From Curiosity to Conjectures
I use Twitter a lot, and on days when I spend more than one hour on it, I feel that I’m more distracted and not as productive as usual. I believe that this is something that many other writers experience. Am I right or am I wrong? Is this just something that I feel or something that is happening to everyone else? Can I transform my hunch into a general claim? For instance, can I say that an X percent increase of Twitter usage a day leads a majority of writers to a Y percent decrease in productivity? After all, I have read some books that make the bold claim that the Internet changes our brains in a negative way.3
What I’ve just done is to notice an interesting pattern, a possible cause-effect relationship (more Twitter = less productivity), and made a conjecture about it. It’s a conjecture that:
- It makes sense intuitively in the light of what we know about the world.
- It is testable somehow.
- It is made of ingredients that are naturally and logically connected to each other in a way that if you change any of them, the entire conjecture will crumble. This will become clearer in just a bit.
These are the requirements of any rational conjecture. Conjectures first need to make sense (even if they eventually end up being wrong) based on existing knowledge of how nature works. The universe of stupid conjectures is infinite, after all. Not all conjectures are born equal. Some are more plausible a priori than others.
My favorite example of conjecture that doesn’t make sense is the famous Sports Illustrated cover jinx. This superstitious urban legend says that appearing on the cover of Sports Illustrated magazine makes many athletes perform worse than they did before.
To illustrate this, I have created Figure 4.1, based on three different fictional athletes. Their performance curve (measured in goals, hits, scores, whatever) goes up, and then it drops after being featured on the cover of Sports Illustrated.
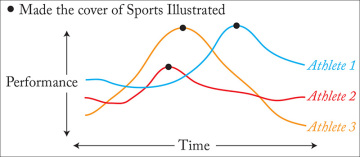
Figure 4.1 Athletes tend to underperform after they’ve appeared on the cover of Sports Illustrated magazine. Does the publication cast a curse on them?
Saying that this is a curse is a bad conjecture because we can come up with a much more simple and natural explanation: athletes are usually featured on magazine covers when they are at the peak of their careers. Keeping yourself in the upper ranks of any sport is not just hard work, it also requires tons of good luck. Therefore, after making the cover of Sports Illustrated, it is more probable that the performance of most athletes will worsen, not improve even more. Over time, an athlete is more likely to move closer to his or her average performance rate than away from it. Moreover, aging plays an important role in most sports.
What I’ve just described is regression toward the mean, and it’s pervasive.4 Here’s how I’d explain it to my kids: imagine that you’re in bed today with a cold. To cure you, I go to your room wearing a tiara of dyed goose feathers and a robe made of oak leaves, dance Brazilian samba in front of you—feel free to picture this scene in your head, dear reader—and give you a potion made of water, sugar, and an infinitesimally tiny amount of viral particles. One or two days later, you feel better. Did I cure you? Of course not. It was your body regressing to its most probable state, one of good health.5
For a conjecture to be good, it also needs to be testable. In principle, you should be able to weigh your conjecture against evidence. Evidence comes in many forms: repeated observations, experimental tests, mathematical analysis, rigorous mental or logic experiments, or various combinations of any of these.6
Being testable also implies being falsifiable. A conjecture that can’t possibly be refuted will never be a good conjecture, as rational thought progresses only if our current ideas can be substituted for better-grounded ones later, when new evidence comes in.
Sadly, we humans love to come up with non-testable conjectures, and we use them when arguing with others. Philosopher Bertrand Russell came up with a splendid illustration of how ludicrous non-testable conjectures can be:
- If I were to suggest that between the Earth and Mars there is a china teapot revolving about the sun in an elliptical orbit, nobody would be able to disprove my assertion provided I were careful to add that the teapot is too small to be revealed even by our most powerful telescopes. But if I were to go on to say that, since my assertion cannot be disproved, it is intolerable presumption on the part of human reason to doubt it, I should rightly be thought to be talking nonsense. (Illustrated magazine, 1952)
Making sense and being testable alone don’t suffice, though. A good conjecture is made of several components, and these need to be hard to change without making the whole conjecture useless. In the words of physicist David Deutsch, a good conjecture is “hard to vary, because all its details play a functional role.” The components of our conjectures need to be logically related to the nature of the phenomenon we’re studying.
Imagine that a sparsely populated region in Africa is being ravaged by an infectious disease. You observe that people become ill mostly after attending religious services on Sunday. You are a local shaman and propose that the origin of the disease is some sort of negative energy that oozes out of the spiritual aura of priests and permeates the temples where they preach.
This is a bad conjecture not just because it doesn’t make sense or isn’t testable. It is testable, actually: when people gather in temples and in the presence of priests, a lot of them get the disease. There, I got my conjecture tested and corroborated!
Not really. This conjecture is bad because we could equally say that the disease is caused by invisible pixies who fly inside the temples, the souls of the departed who still linger around them, or by any other kind of supernatural agent. Changing our premises keeps the body of our conjecture unchanged. Therefore, a flexible conjecture is always a bad conjecture.
It would be different if you said that the disease may be transmitted in crowded places because the agent that provokes it, whether a virus or a bacterium, is airborne. The closer people are to each other, the more likely it is that someone will sneeze, spreading particles that carry the disease. These particles will be breathed by other people and, after reaching their lungs, the agent will spread.
This is a good conjecture because all its components are naturally connected to each other. Take away any of them and the whole edifice of your conjecture will fall, forcing you to rebuild it from scratch in a different way. After being compared to the evidence, this conjecture may end up being completely wrong, but it will forever be a good conjecture.
Hypothesizing
A conjecture that is formalized to be tested empirically is called a hypothesis.
To give you an example (and be warned that not all hypotheses are formulated like this): if I were to test my hunch that using Twitter for too long reduces writers’ productivity, I’d need to explain what I mean by “too long” and by “productivity” and how I’m planning to measure them. I’d also need to make some sort of prediction that I can assess, like “each increase of Twitter usage reduces the average number of words that writers are able to write in a day.”
I’ve just defined two variables. A variable is something whose values can change somehow (yes-no, female-male, unemployment rate of 5.6, 6.8, or 7.1 percent, and so on). The first variable in our hypothesis is “increase of Twitter usage.” We can call it a predictor or explanatory variable, although you may see it called an independent variable in many studies.
The second element in our hypothesis is “reduction of average number of words that writers write in a day.” This is the outcome or response variable, also known as the dependent variable.
Deciding on what and how to measure is quite tricky, and it greatly depends on how the exploration of the topic is designed. When getting information from any source, sharpen your skepticism and ask yourself: do the variables defined in the study, and the way they are measured and compared, reflect the reality that the authors are analyzing?
An Aside on Variables
Variables come in many flavors. It is important to remember them because not only are they crucial for working with data, but later in the book they will also help us pick methods of representation for our visualizations.
The first way to classify variables is to pay attention to the scales by which they’re measured.
Nominal
In a nominal (or categorical) scale, values don’t have any quantitative weight. They are distinguished just by their identity. Sex (male or female) and location (Miami, Jacksonville, Tampa, and so on) are examples of nominal variables. So are certain questions in opinion surveys. Imagine that I ask you what party you’re planning to vote, and the options are Democratic, Republican, Other, None, and Don’t Know.
In some cases, we may use numbers to describe our nominal variables. We may write “0” for male and “1” for female, for instance, but those numbers don’t represent any amount or position in a ranking. They would be similar to the numbers that soccer players display on their back. They exist just to identify players, not to tell you which are better or worse.
Ordinal
In an ordinal scale, values are organized or ranked according to a magnitude, but without revealing their exact size in comparison to each other.
For example, you may be analyzing all countries in the world according to their Gross Domestic Product (GDP) per capita but, instead of showing me the specific GDP values, you just tell me which country is the first, the second, the third, and so on. This is an ordinal variable, as I’ve just learned about the countries’ rankings according to their economic performance, but I don’t know anything about how far apart they are in terms of GDP size.
In a survey, an example of ordinal scale would be a question about your happiness level: 1. Very happy; 2. Happy; 3. Not that happy; 4. Unhappy; 5. Very unhappy.
Interval
An interval scale of measurement is based on increments of the same size, but also on the lack of a true zero point, in the sense of that being the absolute lowest value. I know, it sounds confusing, so let me explain.
Imagine that you are measuring temperature in degrees Fahrenheit. The distance between 5 and 10 degrees is the same as the distance between 20 and 25 degrees: 5 units. So you can add and subtract temperatures, but you cannot say that 10 degrees is twice as hot as 5 degrees, even though 2 × 5 equals 10. The reason is related to the lack of a real zero. The zero point is just an arbitrary number, one like any other on the scale, not an absolute point of reference.
An example of interval scale coming from psychology is the intellectual quotient (IQ). If one person has an IQ of 140 and another person has an IQ of 70, you can say that the former is 70 units larger than the latter, but you cannot say that the former is twice as intelligent as the latter.
Ratio
Ratio scales have all the properties of the other previous scales, plus they also have a meaningful zero point. Weight, height, speed, and so on, are examples of ratio variables. If one car is traveling at 100 mph and another one is at 50, you can say that the first one is going 50 miles faster than the second, and you can also say that it’s going twice as fast. If my daughter’s height is 3 feet and mine is 6 feet (I wish), I am twice as tall as her.
Variables can be also classified into discrete and continuous. A discrete variable is one that can only adopt certain values. For instance, people can only have cousins in amounts that are whole numbers—four or five, that is, not 4.5 cousins. On the other hand, a continuous variable is one that can—at least in theory—adopt any value on the scale of measurement that you’re using. Your weight in pounds can be 90, 90.1, 90.12, 90.125, or 90.1256. There’s no limit to the number of decimal places that you can add to that. Continuous variables can be measured with a virtually endless degree of precision, if you have the right instruments.
In practical terms, the distinction between continuous and discrete variables isn’t always clear. Sometimes you will treat a discrete variable as if it were continuous. Imagine that you’re analyzing the number of children per couple in a certain country. You could say that the average is 1.8, which doesn’t make a lot of sense for a truly discrete variable.
Similarly, you can treat a continuous variable as if it were discrete. Imagine that you’re measuring the distance between galaxy centers. You could use nanometers with an infinite number of decimals (you’ll end up with more digits than atoms in the universe!), but it would be better to use light-years and perhaps limit values to whole units. If the distance between two stars is 4.43457864... light-years, you could just round the figure to 4 light-years.
On Studies
Once a hypothesis is posed, it’s time to test it against reality. I wish to measure if increased Twitter usage reduces book-writing output. I send an online poll to 30 friends who happen to be writers, asking them for the minutes spent on Twitter today and the words they have written. My (completely made up) results are on Figure 4.2. This is an observational study. To be more precise, it’s a cross-sectional study, which means that it takes into account data collected just at a particular point in time.
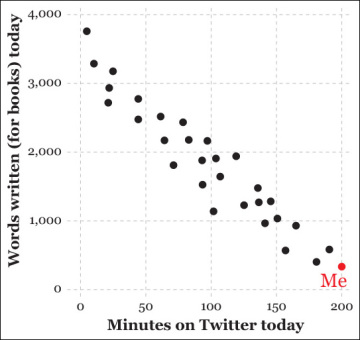
Figure 4.2 Writer friends don’t let their writer friends use Twitter when they are on a deadline.
If I carefully document my friends’ Twitter usage and the pages they write for a long time (a year, a decade, or since Twitter was launched), I’ll have a longitudinal study. On Figure 4.3, I plotted Twitter usage (X-axis) versus words written (Y-axis) every year by three of my 30 fictional author friends. The relationship becomes clear: on average, the more time they spend on Twitter, the less they write for their own books. That’s very unwise!

Figure 4.3 The more writers use Twitter, the fewer words they write. Don’t forget that this is all bogus data.
The choice of what kind of study to conduct depends on many factors. Doing longitudinal studies is usually much more difficult and expensive, as you’ll need to follow the same people for a long time. Cross-sectional studies are faster to build but, in general, their results aren’t very conclusive.7
Going back to my inquiry, I face a problem: I am trying to draw an inference (“writers can benefit from using Twitter less”) from a particular group of writers. That is, I am trying to study something about a population, all writers, based on a sample of those writers, my friends. But are my friends representative of all writers? Are inferences drawn from my sample applicable to the entire population?
Always be suspicious of studies whose samples have not been randomly chosen.8 Not all scientific research is based on random sampling, but analyzing a random sample of writers chosen from the population of all writers will yield more accurate results than a cherry-picked or self-selected sample.
This is why we should be wary of the validity of things like news media online polls. If you ask your audience to opine on a subject, you cannot claim that you’ve learned something meaningful about what the public in general thinks. You cannot even say that you know the opinion of your own audience! You’ve just heard from those readers who feel strongly about the topic you asked about, as they are the ones who are more likely to participate in your poll.
Randomization is useful to deal with extraneous variables, mentioned in Chapter 3 where I advised you to always try to increase depth and breadth. It may be that the results of my current exploration are biased because a good portion of my friends are quite geeky, and so they use Twitter a lot. In this case, the geekiness level, if it could be measured, would distort my model, as it would affect the relationship between predictor and outcome variable.
Some researchers distinguish between two kinds of extraneous variables. Sometimes we can identify an extraneous variable and incorporate it into our model, in which case we’d be dealing with a confounding variable. I know that it may affect my results, so I consider it for my inquiry to minimize its impact. In an example seen in previous chapters, we controlled for population change and for variation in number of motor vehicles when analyzing deaths in traffic accidents.
There’s a second, more insidious kind of extraneous variable. Imagine that I don’t know that my friends are indeed geeky. If I were unaware of this, I’d be dealing with a lurking variable. A lurking variable is an extraneous variable that we don’t include in our analysis for the simple reason that its existence is unknown to us, or because we can’t explain its connection to the phenomenon we’re studying.
When reading studies, surveys, polls, and so on, always ask yourself: did the authors rigorously search for lurking variables and transform them into confounding variables that they can ponder? Or are there other possible factors that they ignored and that may have distorted their results?9
Doing Experiments
Whenever it is realistic and feasible to do so, researchers go beyond observational studies and design controlled experiments, as these can help minimize the influence of confounding variables. There are many kinds of experiments, but many of them share some characteristics:
- They observe a large number of subjects that are representative of the population they want to learn about. Subjects aren’t necessarily people. A subject can be any entity (a person, an animal, an object, etc.) that can be studied in controlled conditions, in isolation from external influences.
- Subjects are divided into at least two groups, an experimental group and a control group. This division will in most cases be made blindly: the researchers and/or the subjects don’t know which group each subject is assigned to.
- Subjects in the experimental group are exposed to some sort of condition, while the control group subjects are exposed to a different condition or to no condition at all. This condition can be, for instance, adding different chemical compounds to fluids and comparing the changes they suffer, or exposing groups of people to different kinds of movies to test how they influence their behavior.
Researchers measure what happens to subjects in the experimental group and what happens to subjects in the control group, and they compare the results.
If the differences between experimental and control groups are noticeable enough, researchers may conclude that the condition under study may have played some role.10
We’ll learn more about this process in Chapter 11.
When doing visualizations based on the results of experiments, it’s important to not just read the abstract of the paper or article and its conclusions. Check if the journal in which it appeared is peer reviewed and how it’s regarded in its knowledge community.11 Then, take a close look at the paper’s methodology. Learn about how the experiments were designed and, in case you don’t understand it, contact other researchers in the same area and ask. This is also valid for observational studies. A small dose of constructive skepticism can be very healthy.

In October 2013, many news publications echoed the results of a study by psychologists David Comer Kidd and Emanuele Castano which showed that reading literary fiction temporarily enhances our capacity to understand other people’s mental states. The media immediately started writing headlines like “Reading fiction improves empathy!”12
The finding was consistent with previous observations and experiments, but reporting on a study after reading just its abstract is dangerous. What were the researchers really comparing?
In one of the experiments, they made two groups of people read either three works of literary fiction or three works of nonfiction. After the readings, the people in the literary fiction group were better at identifying facially expressed emotions than those in the nonfiction group.
The study looked sound to me when I read it, but it left crucial questions in the air: what kinds of literary fiction and nonfiction did the subjects read? It seems predictable that you’ll feel more empathetic toward your neighbor after reading To Kill a Mockingbird than after, say, Thomas Piketty’s Capital in the Twenty-First Century, a brick-sized treaty on modern economics that many bought—myself included—but just a few read.
But what if researchers had compared To Kill a Mockingbird to Katherine Boo’s Behind the Beautiful Forevers, a haunting and emotional piece of journalistic reporting? And, even if they had compared literary fiction with literary nonfiction, is it even possible to measure how “literary” either book is? Those are the kinds of questions that you need to ask either to the researchers that conducted the study or, in case they cannot be reached for comment, to other experts in the same knowledge domain.
About Uncertainty
Here’s a dirty little secret about data: it’s always noisy and uncertain.13
To understand this critical idea, let’s begin with a very simple study. I want to know my weight. I’ve been exercising lately, and I want to check the results. I step on the scale one morning and I read 192 lbs.
Out of curiosity, I decide to weigh myself again the day after. The scale shows 194 lbs. Damn it! How is that even possible? I’ve been eating better and running regularly, and my weight had already dropped from 196.4 lb. There’s surely some sort of discrepancy between the measurements I’m getting and my true weight. I decide to continue weighing myself for more than a month.
The results are in Figure 4.4. There’s a clear downward trend, but it only becomes visible when I display more than five or six days in a row. If I zoom in too much to the chart and just pay attention to two or three days, I’d be fooled into thinking that the noise in the data means something.
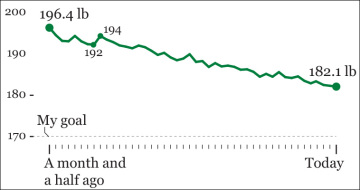
Figure 4.4 Randomness at work—weight change in a month and a half.
There may be different reasons for this wacky fluctuation to happen. My first thought is that my scale may not be working well, but then I realize that if there were some sort of technical glitch, it would bias all my measurements systematically. So the scale is not the source of the fluctuation.
It might be that I don’t always balance my weight equally between my feet or that I’m weighing myself at slightly different times on each day. We tend to be a bit heavier in the afternoon than right after we wake up because we lose water while we sleep, and our body has already processed the food we ate the night before. But I was extremely careful with all those factors. I did weigh myself exactly at 6:45 a.m. every single day. And still, the variation is there. Therefore, I can only conclude that it’s the result of factors that I can’t possibly be aware of. I’m witnessing randomness.
Data always vary randomly because the object of our inquiries, nature itself, is also random. We can analyze and predict events in nature with an increasing amount of precision and accuracy, thanks to improvements in our techniques and instruments, but a certain amount of random variation, which gives rise to uncertainty, is inevitable. This is as true for weight measurements at home as it is true for anything else that you want to study: stock prices, annual movie box office takings, ocean acidity, variation of the number of animals in a region, rainfall or droughts—anything.
If we pick a random sample of 1,000 people to analyze political opinions in the United States, we cannot be 100 percent certain that they are perfectly representative of the entire country, no matter how thorough we are. If our results are that 48.2 percent of our sample are liberals and 51.8 percent are conservatives, we cannot conclude that the entire U.S. population is exactly 48.2 percent liberal and 51.8 percent conservative.
Here’s why: if we pick a completely different random sample of people, the results may be 48.4 percent liberal and 51.6 percent conservative. If we then draw a third sample, the results may be 48.7 percent liberal and 51.3 percent conservative (and so forth).
Even if our methods for drawing random samples of 1,000 people are rigorous, there will always be some amount of uncertainty. We may end up with a slightly higher or lower percentage of liberals or conservatives out of pure chance. This is called sample variation.
Uncertainty is the reason why researchers will never just tell you that 51.8 percent of the U.S. population is conservative, after observing their sample of 1,000 people. What they will tell you, with a high degree of confidence (usually 95 percent, but it may be more or less than that), is that the percentage of conservatives seems to be indeed 51.8 percent, but that there’s an error of plus or minus 3 percentage points (or any other figure) in that number.
Uncertainty can be represented in our visualizations. See the two charts in Figure 4.5, designed by professor Adrian E. Raftery, from the University of Washington. As they display projections, the amount of uncertainty increases with time: the farther away we depart from the present, the more uncertain our projections will become, meaning that the value that the variable “population” could adopt falls inside an increasingly wider range.
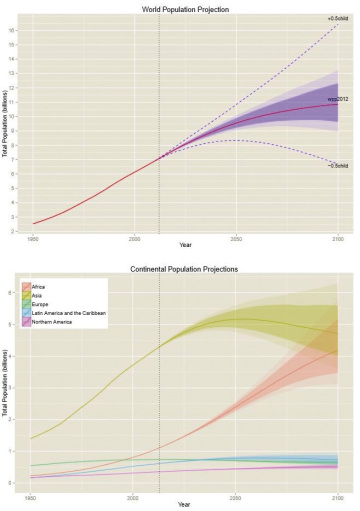
Figure 4.5 Charts by Adrian E. Raftery (University of Washington) who explains, “The top chart shows world population projected to 2100. Dotted lines are the range of error using the older scenarios in which women would have 0.5 children more or less than what’s predicted. Shaded regions are the uncertainties. The darker shading is the 80 percent confidence bars, and the lighter shading shows the 95 percent confidence bars. The bottom chart represents population projections for each continent.” http://www.sciencedaily.com/releases/2014/09/140918141446.htm
The hockey stick chart of world temperatures, in Chapter 2, is another example of uncertainty visualized. In that chart, there’s a light gray strip behind the dark line representing the estimated temperature variation. This gray strip is the uncertainty. It grows narrower the closer we get to the twentieth century because instruments to measure temperature, and our historical records, have become much more reliable.

We’ll return to testing, uncertainty, and confidence in Chapter 11. Right now, after clarifying the meaning of important terms, it’s time to begin exploring and visualizing data.
To Learn More
- Skeptical Raptor’s “How to evaluate the quality of scientific research.” http://www.skepticalraptor.com/skepticalraptorblog.php/how-evaluate-quality-scientific-research/
- Nature magazine’s “Twenty Tips For Interpreting Scientific Claims.” http://www.nature.com/news/policy-twenty-tips-for-interpreting-scientific-claims-1.14183
- Box, George E. P. “Science and Statistics.” Journal of the American Statistical Association, Vol. 71, No. 356. (Dec., 1976), pp. 791-799. Available online: http://www-sop.inria.fr/members/Ian.Jermyn/philosophy/writings/Boxonmaths.pdf
- Prothero, Donald R. Evolution: What the Fossils Say and Why It Matters. New York: Columbia University Press, 2007. Yes, it’s a book about paleontology, but, leaving aside the fact that prehistoric beasts are fascinating, the author offers one of the clearest and most concise introductions to science I’ve read.
