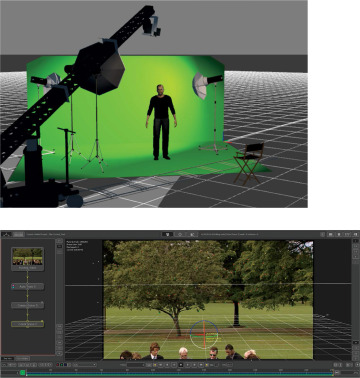
[digital] Visual Effects and Compositing: 3D for VFX
- How 3D CGI Is Created
- 3D Applications
- 3D Motion Tracking
- 3D Matchmoving
VFX have advanced tremendously since their humble stage beginnings as practical special effects in the late 1800s and early 1900s. With the rapid advancements in computer graphics technologies and techniques in the late 1990s and early 2000s, those models, miniatures, and puppets rapidly gave way to the world of 3D CGI (computer-generated imagery). In 3D, anything can be created—from props and digital prosthetics to entire sets and even full 3D worlds.
How 3D CGI Is Created
At the heart of 3D CGI is the concept of representing the 3D world on a 2D screen. To do this, computer software must somehow calculate and simulate points in space in the 3D world in order to draw (or render) points (also known as vertices) and surfaces (whether polygons, surfaces, normal vectors, also called normals, or faces). We VFX artists use a common mathematical 3-axis system to describe our virtual 3D world.
We call this the XYZ coordinate system. Typically X represents the horizontal axis, Y represents the vertical axis, and Z represents the in and out or depth axis. If you are unfamiliar with the XYZ coordinate system, an easy way to remember it is to hold your fingers like a child pretending to shoot a gun, but with your middle finger sticking out at a 90 degree angle (perpendicular) to your pointer finger, as seen in Figure 4.1. With your fingers in this configuration, as silly as it might look to those around you, your middle finger is the X axis, your thumb is the Y axis, and your pointer is the Z axis.

Figure 4.1 Fingers representing the XYZ coordinate system: middle finger (X), thumb (Y), and pointer (Z)
There are a few different methods of creating 3D models, or meshes, but they all work pretty much the same way.
Points (vertices) or curves (also known as splines) are created or placed in the virtual 3D environment (see Figure 4.2). These points or curves are then connected to create edges (Figure 4.3). Edges and splines are then closed to create polygonal faces (sometimes referred to as patches), as shown in Figure 4.4.
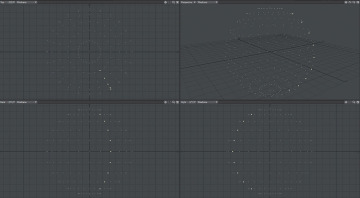
Figure 4.2 Points (vertices) and curves (splines)
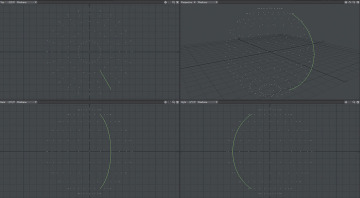
Figure 4.3 Vertices and splines connected with edges
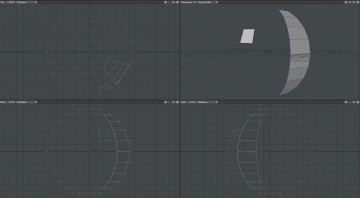
Figure 4.4 Edges and splines closed to create polygonal faces
Primitive 3D shapes can also be created, modified, and combined to more quickly create complex objects, as shown in Figure 4.5.

Figure 4.5 Primitives combined to create complex meshes
For creating hard surface models such as buildings, furniture, computers, and so on, this method of building 3D models works very well. In cases where more curved or fluid shapes are required (called organic modeling), rough or blocky polygonal models’ faces, as shown in Figure 4.6, can be smoothed (or subdivided) to create even more complex shapes and models. This method of creating rough blocky polygonal models and then subdividing them into smooth organic shapes is referred to as subdivision surface modeling.

Figure 4.6 A simple untextured/unsurfaced 3D polygonal sphere
Once faces, or polygons, are created, they can be textured (or surfaced) to create the appearance of real or fictional objects. These textures (or maps) can be any combination of colors, images, or mathematical procedural operations, as discussed in Chapter 2 in the section “Other Matched Texture/Layer/Element Sets.” Textures can then be layered and combined to form complex materials (or shaders).
Texturing (or surfacing) is both an art and a science. The most important skill required for great texturing or surfacing is refining your observational skills. Let’s take a look at a couple examples.
In Figure 4.6 you can see a simple 3D sphere.
By carefully observing the details and attributes of the surfaces of other spherical-based objects, you can easily modify the textures and surface attributes of this simple sphere, changing it into many completely different objects.
First, for a simple one, let’s create the texture of a billiard ball. Billiard balls are colored and have a high-gloss finish. By setting the value in the color channel—in this case, to blue—and the diffuse channel to 90% (which will give the ball 90% of its reflected color from the blue base color in the color channel), the ball will take on a nice, bright, saturated blue finish (as seen in Figure 4.7).

Figure 4.7 3D sphere with Blue selected in the color channel and the diffuse channel set to 90%
Because a billiard ball is also very shiny from the highly polished finish, you want to turn the specular value up very high as well (in Figure 4.8, the specular channel is set to 100%).

Figure 4.8 Specular channel set to 100%
Notice that the specular highlight, or hotspot (the white spot reflection of the light source), is very broad and spread out. The tight molecular structure of a billiard ball’s high-polish finish creates a very tight highlight spot. To simulate this, you can also increase the glossiness channel to 100%, as shown in Figure 4.9.

Figure 4.9 Glossiness set to 100%
That gloss finish means that it is partially reflective. So you can also add a slight amount of reflectivity to the reflection channel, which gives a nice re-creation of a billiard ball’s texture. Of course, for a production, as discussed in Chapter 2, you would want to add the number decal and many imperfections to the surfaces, such as dings and dents in the finish and even chalk marks and fingerprints to dull down the finish in some areas for added realism.
Next, let’s look at the mirrored gazing ball reference image in Figure 4.10.

Figure 4.10 Mirrored gazing ball reference image
From the very first glance you can see that the gazing ball really has no color of its own, but instead, because it is so highly reflective, it gets it color from the reflection of whatever is around it—in this case an outside park scene. By turning the diffuse map to black (or zero), you turn off any base color the sphere would have. You can also set the color map to black since there isn’t any. It too is shiny and glossy, so those aspects should be set high, similar to the way they were set for the billiard ball. Finally, you will want to set the reflection channel to 100% (or close to it) since a mirrored ball is definitely reflective. But something’s wrong! So far your sphere is just a shiny, glossy black. Actually, the only thing that’s wrong is that there’s nothing for your mirrored ball to reflect. When you load the image of the exterior park scene (Figure 4.11) where the reference image was taken into the environment or reflection channel, the 3D mirrored ball instantly springs to life, as you can see in Figure 4.12.

Figure 4.11 A 180-degree spherical image of a park loaded into the environment reflection channel

Figure 4.12 The finished 3D CGI mirrored gazing ball
Now the ball has become a very accurate re-creation of the original. As with the first example, for a production quality model you would want to add all of the similar “reality imperfections.”
Finally, for a completely different spin, let’s create a pumpkin. We’ll push in the top and bottom of the sphere and reset all of the map parameters; then, using the same technique and dirty warehouse floor texture we used in Chapter 2, we’ll create a dirty, desaturated orange texture (Figure 4.13).

Figure 4.13 A dirty desaturated orange texture
Next, since a pumpkin reflects a lot of its own orange color, set the diffuse channel high, to about 80% (to taste of course), the specular channel to about 20% (to give a wide highlight), and the glossiness to between 30 and 40% to emulate the shiny waxy-like surface of a pumpkin. This will give you something that looks like Figure 4.14.

Figure 4.14 The diffuse, specular, and glossiness settings are set.
It’s always important to think about a texture or material thoroughly, the same way you thoroughly need to think through every VFX you create, as described in Chapter 1. If a pumpkin were to have the dirty discolorations that the dirty warehouse floor texture has, it most definitely wouldn’t be as shiny on those spots as on the waxy orange surface of the pumpkin skin itself. To simulate this, you can load a matching copy of one of the dirt/grunge textures used to create the orange skin texture into the specular channel to “knock down” the amount of specularity in those spots, as shown in Figure 4.15. This is called specularity breakup.

Figure 4.15 Specularity breakup added to the specularity (spec) channel
You can now see that those dirty spots are less shiny than the cleaner skin areas. But this still looks more like a partially deflated dirty orange beach ball than a pumpkin. The magic happens in another channel. This channel isn’t actually a “texture” channel per se in the material/surface sense, but instead, it is a texture channel used by the modeling engine to displace, or push, points/vertices around based on the values of a map (yes, the same kind of map we’ve been using for textures. This one we just need to think through to use for 3D displacement instead of 2D displacement). As with a bump map, a displacement map pushes the vertices in the 3D geometry down, or in, wherever the map is darker and up, or out, wherever it’s lighter. Because a pumpkin has organic linear stripe-like vertical indentations, a map with wavy dark vertical lines that gradually fade to white and then gradually back into another wavy black line will push the geometry of the sphere in or out at those vertices on the geometry, respectively, based on how dark or light the map is at any given point. Once this map (Figure 4.16) is loaded into the displacement channel, the deflated sphere magically transforms into a natural looking pumpkin! (Figure 4.17)
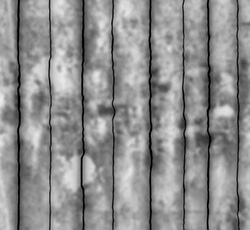
Figure 4.16 Displacement map created to simulate the vertical ridges on a pumpkin

Figure 4.17 The finished, displaced geometry pumpkin