This chapter is from the book
This chapter is from the book
This chapter is from the book
4.3 Spur Gears
Gears are an important and essential mechanical element in mechanical design. A wide range of products and applications use gears. There are various types of gears: spur, helical, bevel, spiral, worm, planetary, and rack and pinion, to name a few. A spur gear is the simplest type of gear and the type we cover here. Typical mechanical design courses in colleges cover the principles and design of gears. In this section, we cover spur gears from a CAD point of view (i.e., how we construct a gear once it is designed). While gears are standard elements that can be purchased off the shelf (they can also be inserted from the SolidWorks Toolbox into a part or assembly file), it is important to learn how to create a gear feature in a CAD/CAM system.
A gear tooth is the intricate part of a gear. Figure 4.3 shows two meshing gears. Figure 4.4A shows the conjugate line and pressure angle. Figure 4.4B shows the involute profile. Gearing and gear meshing ensure that two disks (the two gears) in contact roll against one another without slipping.
Moreover, the gear teeth should not interfere with the uniform rotation that one gear would induce in the other—a requirement known as the conjugate action. The conjugate action also ensures that the perpendicular line to a tooth profile at its point of contact with a tooth from the other gear always passes through a fixed point on the centerline connecting the centers of the two meshing gears. Figure 4.4A shows the conjugate line. The conjugate line is also known as the line of force because the driving force from the driving gear (driver) is transmitted in the direction of this line to the other gear (driven). The angle between the perpendicular radius to the conjugate line and the centerline is always constant for two meshing gears. This angle is known as the pressure angle and is shown as the angle ø in Figure 4.4A.
)
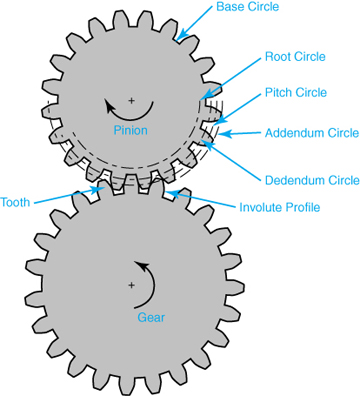
Figure 4.3 Meshing gears
The key to successful functional gears is the conjugate action. While various profiles can produce conjugate action, the involute profile is the best because it allows for imperfections in gear manufacturing and yet maintains the conjugate action. The imperfection may produce a slightly different distance between the two shafts of the gears from the designed value. Figure 4.4B shows how the shape of the involute profile is generated. An involute is defined as the path of the endpoint of a cord when it is pulled straight (held taut) and unwrapped from a circular disk, as shown in Figure 4.4B. The involute geometry ensures that a constant rotational speed of the driving gear produces a constant rotational speed in the driven gear. For spur gears, the teeth are cut perpendicular to the plane of the gear, where the involute profile resides.
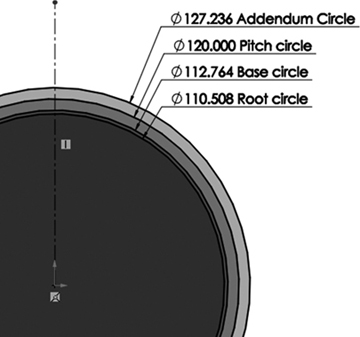
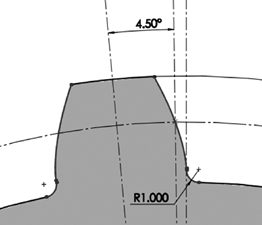
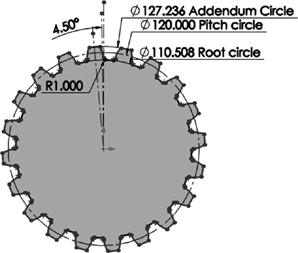
The creation of a gear CAD model requires two basic concepts: knowledge of the gear geometry and the involute equation. The geometry is shown in Figure 4.3. The base circle is the circle where the involute profile begins. The pitch circle defines the contact (pitch) point between the two gears (see Figure 4.4A). The dedendum circle is usually the same as the base circle, as can be concluded from Figure 4.4A (dedendum d = rp – rb). The addendum circle is the circle that defines the top of the tooth as shown in Figure 4.4C (addendum a = ra – rp, where ra is the addendum circle radius). Typically, the addendum and the dedendum are equal. In such case, the pitch and base circle sizes determine the values for both. The root circle is smaller than the base circle to allow cutting the tooth during manufacturing. The tooth profile between the base and root circles is not an involute. It could be any geometry, such as line.
)
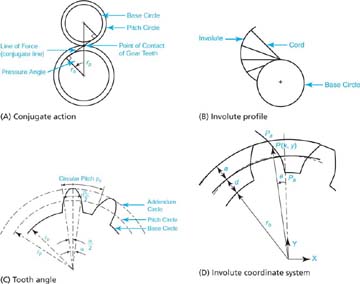
Figure 4.4 Details of a gear tooth
The creation of a gear CAD model requires two steps: Calculate the tooth angle α and the tooth involute profile. While many books on mechanical engineering design offer extensive in-depth coverage of gear analysis, we offer a simplified but accurate version that enables us to create a CAD model of the gear. We begin with the definition of circular pitch. As shown in Figure 4.4C, the circular pitch, pc, is defined as the distance along the pitch circle between corresponding points on adjacent teeth. As shown in Figure 4.4C, we use pc as the circular pitch of the gear, rp as the pitch circle radius, and α as the tooth angle. Using these variables, we can write:
where dp = 2rp is the pitch circle diameter and N is the number of gear teeth. From the tooth geometry shown in Figure 4.4C, we can write:
Substituting pc from Eq. (4.2) into Eq. (4.1) and reducing gives:
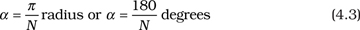
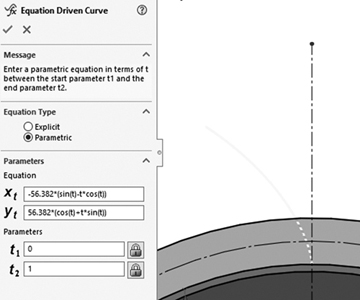
The derivation of the involute equation is more complex and is not covered here. We align the involute of one tooth with the XY coordinate system as shown in Figure 4.4D, where the lowest point Pb on the involute lies on the Y axis. This orientation does not represent a limitation but rather simplifies the form of the involute equation, which is therefore given by:
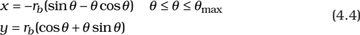
where rb (the base circle radius) is given by (see Figure 4.4A):
and (x, y) are the coordinates of any point P on the involute at an angle θ, as shown in Figure 4.4D. The lowest point Pb on the involute corresponds to the value of θ = 0 and lies on the base circle. Point Pa lies on the addendum circle and does not necessarily correspond to the value of θ = θmax. We can arbitrarily select a large enough value for θmax so that the involute crosses the addendum circle and then trim it to that circle. Therefore, we create the involute profile by generating points on it using Eq. (4.4) and connecting them with a spline curve, or we input Eq. (4.4) into a CAD/CAM system.
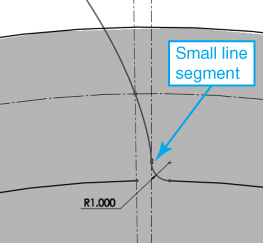
The root circle is always less than the base circle. For simplicity, we have the root circle radius, rr, be 0.98 of the base circle radius. (There are other formulas that do not give consistent results.) Thus, we write:
The following steps summarize the calculations we need to create a gear CAD model:
The input parameters we need are the pitch circle radius rp, the pressure angle Ø, and the gear number of teeth N.
Calculate rb using Eq. (4.5).
Calculate rr using Eq. (4.6).
Calculate the gear dedendum d = rp – rb.
Assuming that the addendum and dedendum are equal, calculate the addendum circle radius as ra = rp + a = rp + d (see Figures 4.4C and 4.4D).
Use Eq. (4.3) to calculate the tooth angle α.
Enter the involute parametric equation given by Eq. (4.4) into a CAD/CAM system to sketch the involute curve as a spline.
Create one gear tooth and use a sketch circular pattern to pattern it to create all gear teeth.
Example 4.2
Create the CAD model of a spur gear with rp = 60 mm, Ø = 20°, and N = 20.
Solution Using the above calculation steps, you get rb = 56.382 mm, d = a = 3.618 mm, ra = 63.618 mm, rr = 55.254 mm, and α = 9°. There are two methods to create the tooth involute curve.
In the first method, you use Eq. (4.4) with Δθ = 5°. You generate 11 points on the involute, for θmax = 50°. You generate the points on the involute curve. You then use Insert > Curve > Curve Through XYZ Points. A better method is to input Eq. (4.4) into SolidWorks and let SolidWorks generate the curve. You need to use radians for the angle θ. You use 1 radian for θmax. This value is arbitrary to ensure that the involute curve intersects and crosses the addendum circle to be able to trim it to the intersection point. Also, SolidWorks uses the parameter t, requiring us to replace θ with t when you input the equation. Figure 4.5 shows the spur gear. You create half a tooth, mirror it to create a full tooth, and use a circular pattern for the full tooth to create all teeth of the gear. Here are the detailed steps.
)
Figure 4.5 Spur gear
Step 1. Create Sketch1 circles and axes: File > New > Part > OK > Front Plane > Circle on Sketch tab > sketch four circles and dimension as shown > Centerline on Sketch tab > sketch vertical line > File > Save As > example4.2 > Save.
Note: Set the part units to mm before you start. The vertical centerline serves as a validation that the involute bottom endpoint passes through it when you create it in Step 2. Also, you will not close the sketch until you finish Step 5.
Step 2. Create Sketch1 tooth involute: Front Plane > Sketch tab > Spline dropdown on Sketch tab > Equation Driven Curve > Parametric > enter x and y equations and limits as shown > ✓.
Step 3. Create Sketch1 tooth bottom: Line on Sketch tab > sketch a line passing through bottom end of involute curve and crossing the root circle > Esc on keyboard > select the line + Ctrl on keyboard + involute curve > Tangent from Add Relations options on left pane > ✓ > Point on Sketch tab > create a point at intersection of involute and pitch circle (turn relations on: View > Sketch Relations to see all) > Centerline on Sketch tab > sketch a line passing through origin and crossing involute at any point > Esc key > select centerline just created + Ctrl + point > Coincident from Add Relations options on left pane > ✓ > Trim Entities on Sketch tab > Trim to closest > select line below root circle and select root circle between two centerlines > ✓ > Fillet on Sketch tab > enter 1 mm for radius > select line and root circle > Yes to continue > ✓ > select base circle > Delete key on keyboard.
Step 4. Create Sketch1 tooth other half: Trim Entities on Sketch tab > Trim to closest > select involute top part > Centerline on Sketch tab > sketch a line passing through origin and to left of involute > Smart Dimension on Sketch tab > select the centerline just created and the other centerline to the right of it > enter 4.5 > ✓ > Mirror Entities on Sketch tab > select involute + Ctrl key + line segment connected to involute + fillet created in Step 3 > click Mirror about box on left of screen > select the far left centerline > ✓ > Trim Entities on Sketch tab > Trim to closest > click addendum circle outside tooth > click root circle inside tooth twice to delete its two segments inside the tooth > ✓.
Step 5. Create Sketch1 all gear teeth: Linear Sketch Pattern dropdown on Sketch tab > Circular Sketch Pattern > click first box under Parameters on left pane > select origin to define axis of pattern > click Entities to Pattern box > select the tooth profile 7 entities > enter 20 for the number of instances to create > ✓ > the sketch becomes over defined when you pattern the tooth because of the profile mirror of first tooth. Click this sequence to resolve it: Over Defined (shown red in status bar) > Diagnose > Accept > Trim Entities > Trim to closest > trim all excess from root circle (segments inside teeth) > ✓ > exit sketch.
Step 6. Create Gear feature: Select Sketch1 > Features tab > Extruded Boss/Base > Enter 25 for D1 > reverse extrusion direction > ✓.
Step 7. Create Sketch2 and Cut-Extrude1-Chamfer: Select Gear front face > Features tab > Extruded Cut > Circle on Sketch tab > click origin and draw circle > select root circle and sketched circle and add Coradial relationship > exit sketch > enter 10 for D1 > check Flip side cut > click Draft icon > enter 60 for Draft Angle > ✓.
Step 8. Create Sketch3 and Cut-Extrude2-Chamfer: Repeat Step 7 but use the back face of Gear.