- Understanding Solid Objects
- Understanding Sketching Techniques
- 3.1 Technique of Lines
- 3.2 Sketching Straight Lines
- 3.3 Sketching Circles, Arcs, and Ellipses
- 3.4 Maintaining Proportions
- 3.5 One-View Drawings
- 3.6 Pictorial Sketching
- 3.7 Projection Methods
- 3.8 Axonometric Projection
- 3.9 Isometric Projection
- 3.10 Isometric Drawings
- 3.11 Making an Isometric Drawing
- 3.12 Offset Location Measurements
- 3.13 Hidden Lines and Centerlines
- 3.14 Angles in Isometric
- 3.15 Irregular Objects
- 3.16 Curves in Isometric
- 3.17 True Ellipses in Isometric
- 3.18 Orienting Ellipses in Isometric Drawings
- 3.19 Drawing Isometric Cylinders
- 3.20 Screw Threads in Isometric
- 3.21 Arcs in Isometric
- 3.22 spheres in Isometric
- 3.23 Oblique Sketches
- 3.24 Length of Receding Lines
- 3.25 Choice of Position in Oblique Drawings
- 3.26 Ellipses for Oblique Drawings
- 3.27 Angles in Oblique Projection
- 3.28 Sketching Assemblies
- 3.29 Sketching Perspectives
- 3.30 Curves and Circles in Perspective
- 3.31 Shading
- 3.32 Computer Graphics
- 3.33 Drawing on Drawing
- Key Words
- Chapter Summary
- Worksheets
- Review Questions
- Sketching Exercises
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.8 Axonometric Projection
The feature that distinguishes axonometric projection from multiview projection is the inclined position of the object with respect to the planes of projection. When a surface or edge of the object is not parallel to the plane of projection, it appears foreshortened. When an angle is not parallel to the plane of projection, it appears either smaller or larger than the true angle.
To create an axonometric view, the object is tipped to the planes of projection so that principal faces, such as the top, side, and front, show in a single view. This produces a pictorial drawing that is easy to visualize, but because the principal edges and surfaces of the object are inclined to the plane of projection, the lengths of the lines are foreshortened. The angles between surfaces and edges appear either larger or smaller than the true angle. There are an infinite variety of ways that the object may be oriented with respect to the plane of projection.
The degree of foreshortening of any line depends on its angle to the plane of projection. The greater the angle, the greater the foreshortening. Once the degree of foreshortening is determined for each of the three edges of the cube that meet at one corner, scales can be easily constructed for measuring along these edges or any other edges parallel to them (Figure 3.34).
)
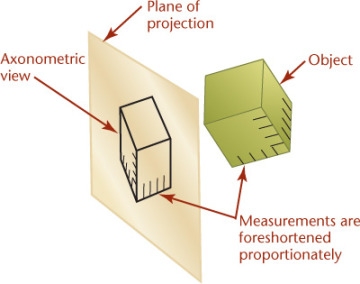
3.34 Measurements are foreshortened proportionately based on the amount of incline.
Use the three edges of the cube that meet at the corner nearest your view as the axonometric axes. Figure 3.35 shows three axonometric projections.
Isometric projection (Figure 3.35a) has equal foreshortening along each of the three axis directions.
Dimetric projection (Figure 3.35b) has equal foreshortening along two axis directions and a different amount of foreshortening along the third axis. This is because it is not tipped an equal amount to all the principal planes of projection.
Trimetric projection (Figure 3.35c) has different foreshortening along all three axis directions. This view is produced by an object that is unequally tipped to all the planes of projection.
)
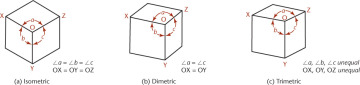
3.35 Axonometric Projections
Axonometric Projections and 3D Models
When you create a 3D CAD model, the object is stored so that vertices, surfaces, and solids are all defined relative to a 3D coordinate system. You can rotate your view of the object to produce a view from any direction. However, your computer screen is a flat surface, like a sheet of paper. The CAD software uses similar projection to produce the view transformations, creating the 2D view of the object on your computer screen. Most 3D CAD software provides a variety of preset isometric viewing directions to make it easy for you to manipulate the view. Some CAD software also allows for easy perspective viewing on screen.
After rotating the object you may want to return to a preset typical axonometric view like one of the examples shown in Figure 3.36.
)
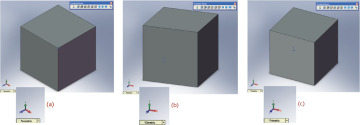
3.36 (a) Isometric View of a 1″ Cube Shown in SolidWorks; (b) Dimetric View; (c) Trimetric View (Images courtesy of ©2016 Dassault Systèmes SolidWorks Corporation.)