Visualization and Sketching
- Understanding Solid Objects
- Understanding Sketching Techniques
- 3.1 Technique of Lines
- 3.2 Sketching Straight Lines
- 3.3 Sketching Circles, Arcs, and Ellipses
- 3.4 Maintaining Proportions
- 3.5 One-View Drawings
- 3.6 Pictorial Sketching
- 3.7 Projection Methods
- 3.8 Axonometric Projection
- 3.9 Isometric Projection
- 3.10 Isometric Drawings
- 3.11 Making an Isometric Drawing
- 3.12 Offset Location Measurements
- 3.13 Hidden Lines and Centerlines
- 3.14 Angles in Isometric
- 3.15 Irregular Objects
- 3.16 Curves in Isometric
- 3.17 True Ellipses in Isometric
- 3.18 Orienting Ellipses in Isometric Drawings
- 3.19 Drawing Isometric Cylinders
- 3.20 Screw Threads in Isometric
- 3.21 Arcs in Isometric
- 3.22 spheres in Isometric
- 3.23 Oblique Sketches
- 3.24 Length of Receding Lines
- 3.25 Choice of Position in Oblique Drawings
- 3.26 Ellipses for Oblique Drawings
- 3.27 Angles in Oblique Projection
- 3.28 Sketching Assemblies
- 3.29 Sketching Perspectives
- 3.30 Curves and Circles in Perspective
- 3.31 Shading
- 3.32 Computer Graphics
- 3.33 Drawing on Drawing
- Key Words
- Chapter Summary
- Worksheets
- Review Questions
- Sketching Exercises
In this sample chapter from Modern Graphics Communicaiton, 5th Edition, learn how to visualize and sketch objects in three dimensions to communicate your ideas quickly and accurately.
Refer to the following standard:
ANSI/ASME Y14.3 Orthographic and Pictorial Views
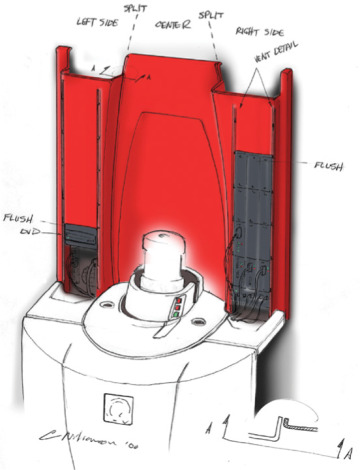
Shaded Sketch Showing Details of Wire Placement (Courtesy of Quantum Design.)
Understanding Solid Objects
Sketches and drawings are used to communicate or record ideas about the shape of 3D objects. Before starting to sketch, it helps to develop a vocabulary for understanding and discussing 3D shapes.
Three-dimensional figures are referred to as solids. Solids are bounded by the surfaces that contain them. These surfaces can be one of the following four types:
Planar
Single curved
Double curved
Warped
Regardless of how complex a solid may be, it is composed of combinations of these basic types of surfaces. Figure 3.1 shows examples of the four basic types of surfaces.
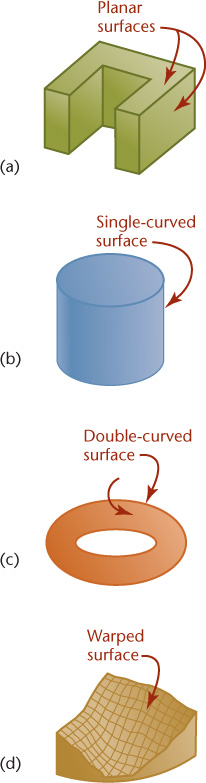
3.1 Types of Surfaces
Types of Solids
Polyhedra
Solids that are bounded by plane surfaces are called polyhedra (Figures 3.2–3.4). These planar surfaces are also referred to as faces of the object. A polygon is a planar area that is enclosed by straight lines.

3.2 Regular Polyhedra
Regular Polyhedra
If the faces of a solid are equal regular polygons, it is called a regular polyhedron. There are five regular polyhedra: the tetrahedron, hexahedron, octahedron, dodecahedron, and icosahedron (Figure 3.2).
Prisms
A prism has two bases, which are parallel equal polygons, and three or more additional faces, which are parallelograms (Figure 3.3). A triangular prism has triangular bases, a rectangular prism has rectangular bases, and so on. (If a prism’s bases happen to be parallelograms, the prism is a called a parallelepiped, a word rarely heard in everyday conversation.)
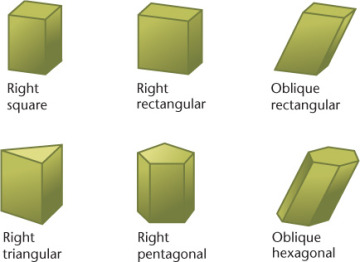
3.3 Right Prisms and Oblique Prisms
A right prism has faces and lateral (side) edges that are perpendicular to the bases; an oblique prism has faces and lateral edges that are angled to the bases. If one end is cut off to form an end that is not parallel to the bases, the prism is said to be truncated (a word that simply means “shortened by having a part cut off”).
Pyramids
A pyramid has a polygon for a base and triangular lateral faces that intersect at a common point called the vertex (Figure 3.4). The line from the center of the base to the vertex is called the axis. If the axis is perpendicular to the base, the pyramid is called a right pyramid; otherwise, it is an oblique pyramid. A triangular pyramid has a triangular base, a square pyramid has a square base, and so on. If a portion near the vertex has been cut off, the pyramid is truncated, or it is referred to as a frustum.
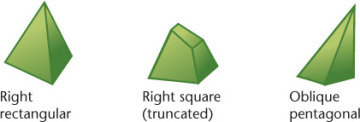
3.4 Pyramids
Cylinders
A cylinder has a single-curved exterior surface (Figure 3.5). You can think of a cylinder as being formed by taking a straight line and moving it in a circular path to enclose a volume. Each position of this imaginary straight line in its path around the axis is called an element of the cylinder.
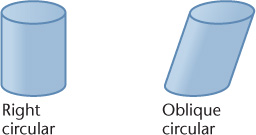
3.5 Cylinder and Oblique Cylinder
Cones
A cone has a single-curved exterior surface (Figure 3.6). You can think of it as being formed by moving one end of a straight line around a circle while keeping the other end fixed at a point, the vertex of the cone. An element of the cone is any position of this imaginary straight line.

3.6 Cones
Spheres
A sphere has a double-curved exterior surface (Figure 3.7). You can think of it as being formed by revolving a circle about one of its diameters, somewhat like spinning a coin. The poles of the sphere are the points at the top and bottom of the sphere that would not move while it was spinning. The axis of the sphere is the term for the line between its poles.

3.7 Sphere
Tori
A torus is shaped like a doughnut (Figure 3.8). Its boundary surface is double curved. You can think of it as being formed by revolving a circle (or other curve) around an axis that is positioned away from (outside) the curve.

3.8 Torus
Ellipsoids
An oblate or prolate ellipsoid is shaped like an egg (Figure 3.9). You can think of it as being formed by revolving an ellipse about its minor or major axis, respectively.
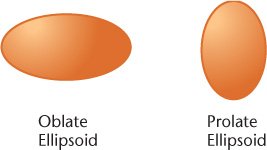
3.9 Ellipsoids