- Understanding Solid Objects
- Understanding Sketching Techniques
- 3.1 Technique of Lines
- 3.2 Sketching Straight Lines
- 3.3 Sketching Circles, Arcs, and Ellipses
- 3.4 Maintaining Proportions
- 3.5 One-View Drawings
- 3.6 Pictorial Sketching
- 3.7 Projection Methods
- 3.8 Axonometric Projection
- 3.9 Isometric Projection
- 3.10 Isometric Drawings
- 3.11 Making an Isometric Drawing
- 3.12 Offset Location Measurements
- 3.13 Hidden Lines and Centerlines
- 3.14 Angles in Isometric
- 3.15 Irregular Objects
- 3.16 Curves in Isometric
- 3.17 True Ellipses in Isometric
- 3.18 Orienting Ellipses in Isometric Drawings
- 3.19 Drawing Isometric Cylinders
- 3.20 Screw Threads in Isometric
- 3.21 Arcs in Isometric
- 3.22 spheres in Isometric
- 3.23 Oblique Sketches
- 3.24 Length of Receding Lines
- 3.25 Choice of Position in Oblique Drawings
- 3.26 Ellipses for Oblique Drawings
- 3.27 Angles in Oblique Projection
- 3.28 Sketching Assemblies
- 3.29 Sketching Perspectives
- 3.30 Curves and Circles in Perspective
- 3.31 Shading
- 3.32 Computer Graphics
- 3.33 Drawing on Drawing
- Key Words
- Chapter Summary
- Worksheets
- Review Questions
- Sketching Exercises
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.9 Isometric Projection
In an isometric projection, all angles between the axonometric axes are equal. To produce an isometric projection, you orient the object so that its principal edges (or axes) make equal angles with the plane of projection and are therefore foreshortened equally. Oriented this way, the edges of a cube are projected so that they all measure the same and make equal angles (of 120°) with each other, as shown in Figure 3.37.
){kind=link}
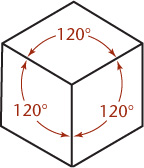
3.37 Isometric Projection
Isometric Axes
The projections of the edges of a cube make angles of 120° with each other. You can use these as the isometric axes from which to make measurements. Any line parallel to one of these is called an isometric line. The angles in the isometric projection of the cube are either 120° or 60°, and all are projections of 90° angles. In an isometric projection of a cube, the faces of the cube, and any planes parallel to them, are called isometric planes. See Figure 3.38.
){kind=link}
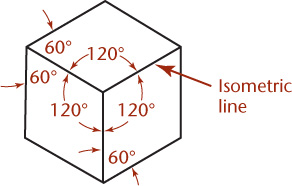
3.38 Isometric Axes
Nonisometric Lines
Lines of an isometric drawing that are not parallel to the isometric axes are called nonisometric lines (Figure 3.39). Only lines of an object that are drawn parallel to the isometric axes are equally foreshortened. Nonisometric lines are drawn at other angles and are not equally foreshortened. Therefore the lengths of features along nonisometric lines cannot be measured directly with a scale.
){kind=link}
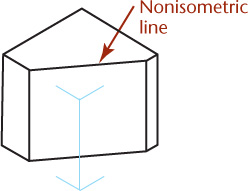
3.39 Nonisometric Edges
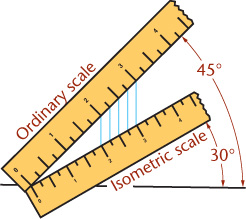
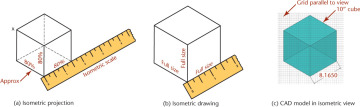
Isometric Scales
An isometric scale can be used to draw correct isometric projections. All distances in this scale are 2/3 × true size, or approximately 80% of true size. Figure 3.40a shows an isometric scale. More commonly, an isometric sketch or drawing is created using a standard scale, as in Figure 3.40b, disregarding the foreshortening that the tipped surfaces would produce in a true projection. Figure 3.40c shows an isometric view of a 10″ cube modeled in 3D. When measured parallel to the view, the length appears to be 8.1650 due to the foreshortening (near 80% of the actual size).
)
3.40 Isometric and Ordinary Scales
TIP: Making an Isometric Scale
You can make an isometric scale from a strip of paper or cardboard by placing an ordinary scale at 45° to a horizontal line and the paper (isometric) scale at 30° to the horizontal line. To mark the increments on the isometric scale, draw straight lines (perpendicular to the horizontal line) from the division lines on the ordinary scale.
Alternatively, you can approximate an isometric scale. Scaled measurements of 9″ = 1′–0, or three-quarter-size scale (or metric equivalent) can be used as an approximation.
