- Understanding Solid Objects
- Understanding Sketching Techniques
- 3.1 Technique of Lines
- 3.2 Sketching Straight Lines
- 3.3 Sketching Circles, Arcs, and Ellipses
- 3.4 Maintaining Proportions
- 3.5 One-View Drawings
- 3.6 Pictorial Sketching
- 3.7 Projection Methods
- 3.8 Axonometric Projection
- 3.9 Isometric Projection
- 3.10 Isometric Drawings
- 3.11 Making an Isometric Drawing
- 3.12 Offset Location Measurements
- 3.13 Hidden Lines and Centerlines
- 3.14 Angles in Isometric
- 3.15 Irregular Objects
- 3.16 Curves in Isometric
- 3.17 True Ellipses in Isometric
- 3.18 Orienting Ellipses in Isometric Drawings
- 3.19 Drawing Isometric Cylinders
- 3.20 Screw Threads in Isometric
- 3.21 Arcs in Isometric
- 3.22 spheres in Isometric
- 3.23 Oblique Sketches
- 3.24 Length of Receding Lines
- 3.25 Choice of Position in Oblique Drawings
- 3.26 Ellipses for Oblique Drawings
- 3.27 Angles in Oblique Projection
- 3.28 Sketching Assemblies
- 3.29 Sketching Perspectives
- 3.30 Curves and Circles in Perspective
- 3.31 Shading
- 3.32 Computer Graphics
- 3.33 Drawing on Drawing
- Key Words
- Chapter Summary
- Worksheets
- Review Questions
- Sketching Exercises
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.27 Angles in Oblique Projection
When an angle that is specified in degrees lies in a receding plane, convert the angle into linear measurements to draw the angle in an oblique drawing. Figure 3.65a shows a drawing with an angle of 30° specified.
)
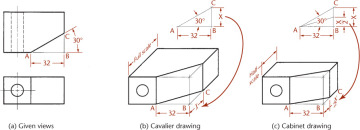
3.65 Angles In Oblique Projection
To draw the angle in the oblique drawing, you will need to know distance X. The distance from point A to point B is given as 32 mm. This can be measured directly in the cavalier drawing (Figure 3.65b). Find distance X by drawing the right triangle ABC (Figure 3.65c) using the dimensions given, which is quick and easy using CAD.
You can also use a mathematical solution to find the length of the side: The length of the opposite side equals the tangent of the angle times the length of the adjacent side. In this case, the length of the opposite side, X, is about 18.5 mm. Draw the angle in the cavalier drawing using the found distance.
Remember that all receding dimensions must be reduced to match the scale of the receding axis. In the cabinet drawing in Figure 3.65c, the distance BC must be half the side BC of the right triangle in Figure 3.65c.
STEP by STEP: USING BOX CONSTRUCTION TO CREATE AN OBLIQUE DRAWING
Follow these steps to draw a cavalier drawing of the rectangular object shown in the two orthographic views.
Lightly block in the overall width (A) and height (B) to form the enclosing rectangle for the front surface. Select an angle for the receding axis (OZ) and draw the depth (C) along it.
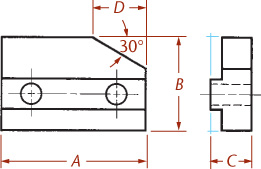
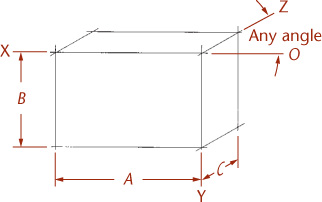
Lightly block in the details of the front surface shape including the two holes, which will appear round. Add the details of the right-side surface shape. Extend lines along the receding axis connecting the edges to form the remaining surface edges.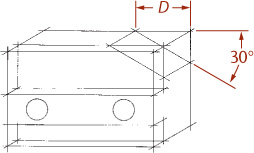
Darken the final lines.
STEP by STEP: USING SKELETON CONSTRUCTION IN OBLIQUE DRAWING
Oblique drawings are especially useful for showing objects that have cylindrical shapes built on axes or centerlines. Follow these steps to construct an oblique drawing of the part shown using projected centerlines.
)
Position the object in the drawing so that the circles shown in the given top view are parallel to the plane of projection. The circles will show true shape in the oblique view. Draw the circular shape in the front plane of the oblique view and extend the center axis along the receding axis of the oblique drawing.
Add the centerline skeleton as shown.
Build the drawing from the location of these centerlines.
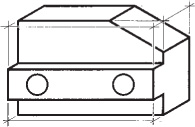
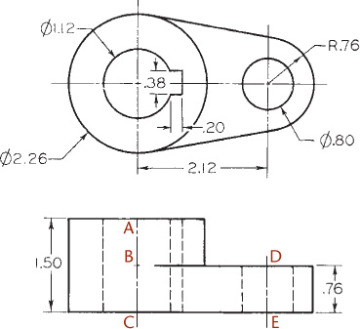
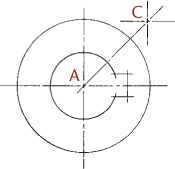
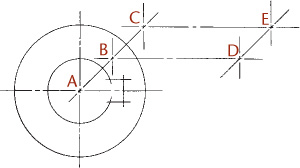
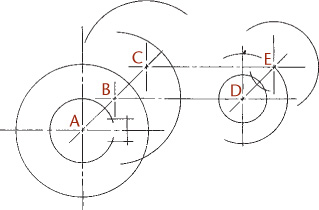
Construct all important points of tangency.
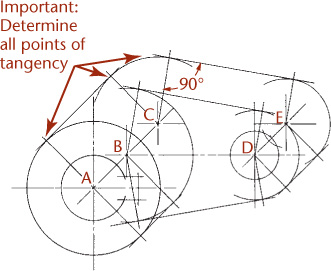
Darken the final cavalier drawing.
