- Coordinates for 3D CAD Modeling
- Geometric Entities
- 4.1 Manually Bisecting a Line or Circular Arc
- 4.2 Drawing Tangents to Two Circles
- 4.3 Drawing an Arc Tangent to a Line or Arc and Through a Point
- 4.4 Bisecting an Angle
- 4.5 Drawing a Line through a Point and Parallel to a Line
- 4.6 Drawing a Triangle with Sides Given
- 4.7 Drawing a Right Triangle with Hypotenuse and One Side Given
- 4.8 Laying Out an Angle
- 4.9 Drawing an Equilateral Triangle
- 4.10 Polygons
- 4.11 Drawing a Regular Pentagon
- 4.12 Drawing a Hexagon
- 4.13 Ellipses
- 4.14 Spline Curves
- 4.15 Geometric Relationships
- 4.16 Solid Primitives
- 4.17 Recognizing Symmetry
- 4.18 Extruded Forms
- 4.19 Revolved Forms
- 4.20 Irregular Surfaces
- 4.21 User Coordinate Systems
- 4.22 Transformations
- Key Words
- Chapter Summary
- Skills Summary
- Review Questions
- Chapter Exercises
This chapter is from the book
This chapter is from the book
This chapter is from the book
4.14 Spline Curves
Splines are used to describe complex, or freeform, curves. Many surfaces cannot be easily defined using simple curves such as circles, arcs, or ellipses. For example, the flowing curves used in automobile design blend many different curves into a smooth surface. Creating lifelike shapes and aerodynamic forms may require spline curves (Figure 4.40).
)
4.40 Complex Curves. The organic shape of this flowerlike bowl was created using SolidWorks splines. Splines can be controlled in a variety of ways. The enlarged view shows the curvature combs used to view the effect of the controlling curves that make up the spline. Dragging a control handle changes the direction of the curve at the control vertex. (Courtesy of Robert Kincaid.)
The word spline originally described a flexible piece of plastic or rubber used to draw irregular curves between points. Mathematical methods generate the points on the curve for CAD applications.
One way to create an irregular curve is to draw curves between each set of points. The points and the tangencies at each point are used in a polynomial equation that determines the shape of the curve. This type of curve is useful in the design of a ship’s hull or an aircraft wing. Because this kind of irregular curve passes through all the points used to define the curve, it is sometimes called an interpolated spline or a cubic spline. An example and its vertices are shown in Figure 4.41.
)
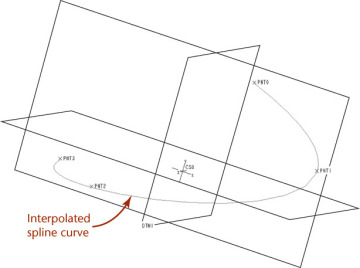
4.41 Interpolated Spline. An interpolated spline curve passes through all the points used to define the curve.
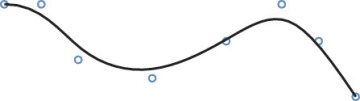
Other spline curves are approximated: they are defined by a set of vertices. The resulting curve does not pass through all the vertices. Instead, the vertices “pull” the curve in the direction of the vertex. Complex curves can be created with relatively few vertices using approximation methods. Figure 4.42 shows a 3D approximated spline curve and its vertices.
){kind=link}
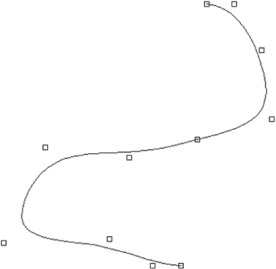
4.42 Approximated Spline. Except for the beginning and endpoints, the fit points for the spline curve stored in the database do not always lie on the curve. They are used to derive the curve mathematically.
The mathematical definition for this type of spline curve uses the X- and Y- (and Z- for a 3D shape) coordinates and a parameter, generally referred to as u. A polynomial equation is used to generate functions in u for each point used to specify the curve. The resulting functions are then blended to generate a curve that is influenced by each point specified but not necessarily coincident with any of them.
Spotlight: B-Splines
The Bezier curve was one of the first methods to use spline approximation to create flowing curves in CAD applications. The first and last vertices are on the curve, but the rest of the vertices contribute to a blended curve between them. The Bezier method uses a polynomial curve to approximate the shape of a polygon formed by the specified vertices. The order of the polynomial is 1 degree less than the number of vertices in the polygon (see Figure 4.43).
)
4.43 Bezier Curve. A Bezier curve passes through the first and last vertex but uses the other vertices as control points to generate a blended curve.
The Bezier method is named for Pierre Bezier, a pioneer in computer-generated surface modeling at Renault, the French automobile manufacturer. Bezier sought an easier way of controlling complex curves, such as those defined in automobile surfaces. His technique allowed designers to shape natural-looking curves more easily than they could by specifying points that had to lie on the resulting curve, yet the technique also provided control over the shape of the curve. Changing the slope of each line segment defined by a set of vertices adjusts the slope of the resulting curve (see Figure 4.44). One disadvantage of the Bezier formula is that the polynomial curve is defined by the combined influence of every vertex: a change to any vertex redraws the entire curve between the start point and endpoint.
)
4.44 Editing a Bezier Curve. Every vertex contributes to the shape of a Bezier curve. Changing the location of a single vertex redraws the entire curve.
A B-spline approximation is a special case of the Bezier curve that is more commonly used in engineering to give the designer more control when editing the curve. A B-spline is a blended piecewise polynomial curve passing near a set of control points. The spline is referred to as piecewise because the blending functions used to combine the polynomial curves can vary over the different segments of the curve. Thus, when a control point changes, only the piece of the curve defined by the new point and the vertices near it change, not the whole curve (see Figure 4.45). B-splines may or may not pass through the first and last points in the vertex set. Another difference is that for the B-spline the order of the polynomial can be set independently of the number of vertices or control points defining the curve.
)
4.45 B-Spline Approximation. The B-spline is constructed piecewise, so changing a vertex affects the shape of the curve near only that vertex and its neighbors.
In addition to being able to locally modify the curve, many modelers allow sets of vertices to be weighted differently. The weighting, sometimes called tolerance, determines how closely the curve should fit the set of vertices. Curves can range from fitting all the points to being loosely controlled by the vertices. This type of curve is called a nonuniform rational B-spline, or NURBS curve. A rational curve (or surface) is one that has a weight associated with each control point.
Splines are drawn in CAD systems based on the mathematical relationships defining their geometry. Figure 4.46 shows an approximated spline drawn using AutoCAD. Figure 4.47 shows an interpolated spline drawn using SolidWorks. Both curves are drawn with a spline command, and both provide a dialog box that allows you to change properties defining the curve; however, the properties that are controlled vary by the type of spline being created by the software package. You should be familiar with the terms used by your modeling software for creating different types of spline curves.
)
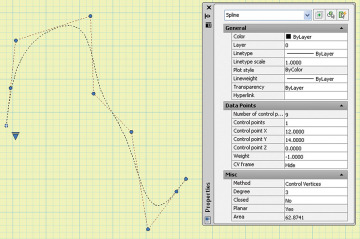
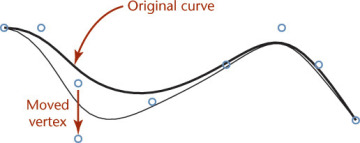
4.46 Approximated Spline. This spline drawn in AutoCAD is pulled toward the defined control points. The Properties dialog box at the right allows you to change the weighting factor for each control point. (Autodesk screen shots reprinted courtesy of Autodesk, Inc.)
)
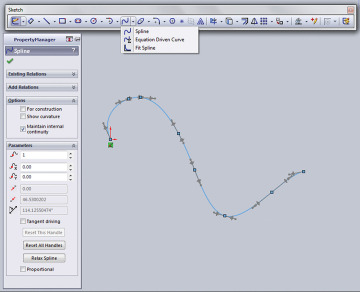
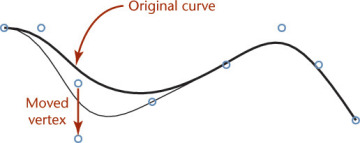
4.47 Interpolated Spline. This SolidWorks spline passes through each control point. Software tools allow you to control spline properties. (Image courtesy of ©2016 Dassault Systèmes SolidWorks Corporation.)