- Understanding Solid Objects
- Understanding Sketching Techniques
- 3.1 Technique of Lines
- 3.2 Sketching Straight Lines
- 3.3 Sketching Circles, Arcs, and Ellipses
- 3.4 Maintaining Proportions
- 3.5 One-View Drawings
- 3.6 Pictorial Sketching
- 3.7 Projection Methods
- 3.8 Axonometric Projection
- 3.9 Isometric Projection
- 3.10 Isometric Drawings
- 3.11 Making an Isometric Drawing
- 3.12 Offset Location Measurements
- 3.13 Hidden Lines and Centerlines
- 3.14 Angles in Isometric
- 3.15 Irregular Objects
- 3.16 Curves in Isometric
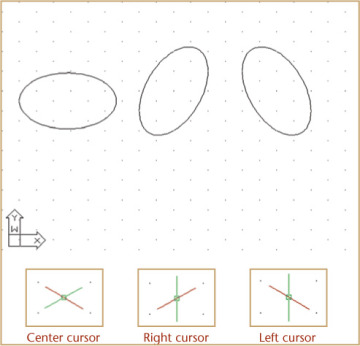
- 3.17 True Ellipses in Isometric
- 3.18 Orienting Ellipses in Isometric Drawings
- 3.19 Drawing Isometric Cylinders
- 3.20 Screw Threads in Isometric
- 3.21 Arcs in Isometric
- 3.22 spheres in Isometric
- 3.23 Oblique Sketches
- 3.24 Length of Receding Lines
- 3.25 Choice of Position in Oblique Drawings
- 3.26 Ellipses for Oblique Drawings
- 3.27 Angles in Oblique Projection
- 3.28 Sketching Assemblies
- 3.29 Sketching Perspectives
- 3.30 Curves and Circles in Perspective
- 3.31 Shading
- 3.32 Computer Graphics
- 3.33 Drawing on Drawing
- Key Words
- Chapter Summary
- Worksheets
- Review Questions
- Sketching Exercises
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.22 spheres in Isometric
The isometric drawing of any curved surface can be constructed from all lines that can be drawn on that surface. For spheres, select the great circles (circles cut by any plane through the center) as the lines on the surface. Because all great circles, except those that are perpendicular or parallel to the plane of projection, are shown as ellipses having equal major axes, they enclose a circle whose diameter is the major axis of the ellipse.
Figure 3.54 shows two given views of a sphere enclosed in a construction cube. Next, an isometric of a great circle is drawn in a plane parallel to one face of the cube. There is no need to draw the ellipse, since only the points on the diagonal located by measurements a are needed to establish the ends of the major axis and thus to determine the radius of the sphere.
)
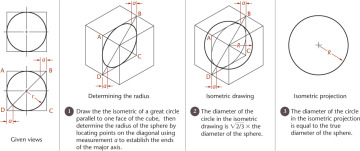
3.54 Isometric of a Sphere
In the resulting isometric drawing, the diameter of the circle is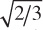 
times the actual diameter of the sphere. The isometric projection is simply a circle whose diameter is equal to the true diameter of the sphere.
STEP by STEP: ISOMETRIC SKETCHING FROM AN OBJECT
Positioning the Object
To make an isometric sketch from an actual object, first hold the object in your hand and tilt it toward you, as shown in the illustration. In this position the front corner will appear vertical. The two receding bottom edges and those edges parallel to them should appear to be at about 30° with horizontal. The steps for sketching the object follow.
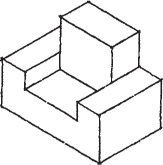
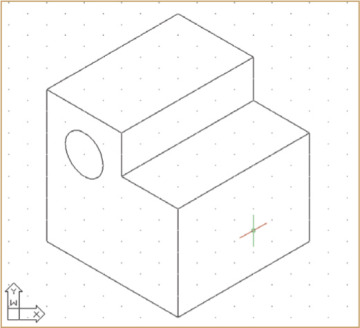
Sketch the enclosing box lightly, making AB vertical and AC and AD approximately 30° with horizontal. These three lines are the isometric axes. Make AB, AC, and AD approximately proportional in length to the actual corresponding edges on the object. Sketch the remaining lines parallel to these three lines.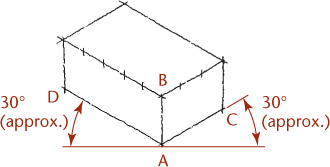
Block in the recess and the projecting block.
Darken all final lines.
CAD at WORK: ISOMETRIC SKETCHES USING AUTOCAD SOFTWARE
Need a quick isometric sketch? AutoCAD software has special drafting settings for creating an isometric style grid.
Figure A shows the Drafting Settings dialog box in AutoCAD. When you check the button for Isometric snap, the software calculates the spacing needed for an isometric grid. You can use it to make quick pictorial sketches like the example shown in Figure B. Piping diagrams are often done this way, although they can also be created using 3D tools.
)
(A) Selecting Isometric Snap in the AutoCAD Drafting Settings Dialog Box (Autodesk screen shots reprinted courtesy of Autodesk, Inc.)
Even though the drawing in Figure B looks 3D, it is really drawn in a flat 2D plane. You can observe this if you change the viewpoint so you are no longer looking straight onto the view.
)
(B) A Pictorial Sketch Created from a Flat Drawing Using Isometric Snap
The Ellipse command in AutoCAD has a special Isocircle option that makes drawing isometric ellipses easy. The isocircles are oriented in different directions depending on the angle of the snap cursor. Figure C shows isocircles and snap cursors for the three different orientations. In the software, you press <Ctrl> and E simultaneously to toggle the cursor appearance.
)
(C) Variously Oriented Isometric Circles and the Corresponding Snap Cursors Used to Create Them